




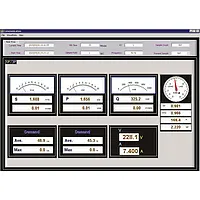
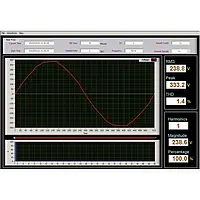

The Clamp on Tester (Graphic Power Quality Analyzer) PCE-GPA 62 is used for single-phase or three-phase measurements of the active, reactive and apparent power, power factor, phase angle, energy, voltage, current as well as peaks and harmonics up to 50º of the harmonic waveform. The Clamp on Tester comes with a built-in graphic display to show network analyzer values. Measured values can be both recorded and transferred to a PC for further analysis. The Clamp on Tester is a professional handheld device to determine several parameters. Thanks to the back light display, it is possible to get an accurate reading of measured values even with poor light conditions. Although the Clamp on Tester comes calibrated from the manufacturer, an optional laboratory calibration and certificate, that meets ISO standards, can be ordered separately with the device or when an annual recalibration is required.
| Voltage measurement | 4.0 ... 600.0 V RMS value ± 0.5% of the measured value ± 5 digits / 0.1 V |
| Voltage peaks (> 10V) | 50 Hz - 60 Hz / ± 5% ± 50 digits |
| Current measurements | 4.0 ... 1500.0 A real ± 1% V. of the measured value ± 5 digits / 0.01 A |
| Current peaks (> 20A) | 50 Hz - 60 Hz / ± 5% ± 50 digits |
| Active power P | 10 W ...
9999 kW in 5 measurement ranges ± 1% of the value + 20 digits (>20 V y >20 A) ± 2% of the value + 40 digits (>20 V y >20 A) 0.1 W ... 1 kW according to the measurement range |
| Apparent power S | 10 VA ...
9999 kVA in 5 measurement ranges ± 1% of the value + 20 digits (>20 V y >20 A) ± 2% of the value + 40 digits (>20 V y >20 A) 0.1 VA ... 1 kVA according to the measurement range |
| Reactive power Q | 10 VAr ...
9999 kVAr in 5 measurements ranges ± 1% of the value + 20 digits (>20 V y >20 A) ± 2% of the value + 40 digits (>20 V y >20 A) 0.1 VAr ... 1 kVAr according to the measurement range |
| PF power factor | 0.000 ...
1.000 ± 0.04 (>20 V >20 A) / 0,001 ± 0.1 (>20 V >20 A) / 0,001 |
| Phase angle | -180 ...
+180 / ±1 / 0,1 0 ... +360 / ±1 / 0,1 |
| Frequency measurement (U > 50 V) | 46 ... 65
Hz ±0.3 Hz / 0.1 Hz |
| Active energy | 0 ...
999.999 kWh ± 1% of the value + 20 digits |
| Apparent energy | 0 ...
999.999 kVAh ± 1% of the value + 20 digits |
| Reactive energy | 0 ...
999.999 kVarh ± 1% of the value + 20 digits |
| Harmonics in the voltage
(relative) 50 - 60 Hz > 80 V AC |
1 - 20 th /
± 2% / 0.1% 21 - 50 th / ± 4% of the value ± 2% / 0.1% |
| Harmonics in the voltage
(absolute) 50 - 60 Hz > 80 V AC |
1 - 20 th /
± 2% / 0.1% 21 - 50 th / ± 4% of the value ± 0.5% / 0.1% |
| Harmonics in the current
(relative) 50 - 60 Hz > 80 V AC |
1 - 20 th /
± 2% / 0.1 % 21 - 50 th / ± 4% of the value ± 2% / 0.1 % |
| Harmonics in the current
(absolute) 50 - 60 Hz > 80 V AC |
1 - 20 th /
± 2% of the value ± 0.4 A / 0.1 A 21 - 50 th / ± 4% of the value ± 0.4 A / 0.1 A |
| Total harmonic
distortion (THD-F) 50 - 60 Hz > 80 V y > 20 A |
0.0 - 20%
/ 2% / 0.1% 20.1 - 100% / ± 6% of the value ± 1% / 0.1% 100.1 - 999.9 % / ± 10% of the value ± 1% / 0.1% |
| Max. clamp opening | 55 mm / 2.2 in |
| Range selection | Auto |
| Overload indication | "OL = Overload |
| Memory | 50,000 readings |
| Interface | USB |
| Software and data cable | included
in the delivery. They can be used with Win 2000, XP, ME |
| Display | graphic LCD display, 128 x 64 with backlight |
| Power supply | 2x 1.5V AA batteries |
| Energy consumption | Approx. 10-mA |
| Dimensions | 271 x 112 x 46 mm / 10.6 x 4.4 x 1.8 in |
| Weight | 650 g / 1.4 lbs with batteries |
| Operating conditions | 85% max. R.H. / -10 ... 50°C / 14 ... 122°F |
| Protection / Standards | CAT III 600 V / EN 61010-2-032 |